9.1 Sequences
Infinite sequence- is a function whose domain is set of positive int
egers.
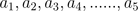
Finding the terms of a sequence
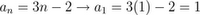
n Factorial
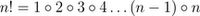
special case 0!=1
Factorial problems
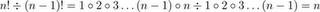
Sigma Notation
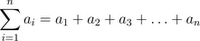
9.2 Arithmetic Sequences and Partial Sums
A sequence is arithmetic if the differences between consecutive terms are the same.
The common difference (d) is the difference be
tween two consecutive numbers in the sequence.
Example:
4, 8, 11, 14, 17,...
d=3
Sum of a Finite Arithmetic Sequence...
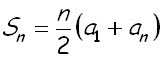
9.3 Geometric Sequences and Series
A Geometric Sequence is the ratios of consecutive terms that are the same.
r is the common ratios
The sum of Geometric Sequences
if r is less that absolute value 1 then the equation is
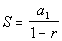
9.5 Binomial Theorem
Binomial- a polygon that has two terms. 
Expanding:
(x + y)¹ = 1x + 1y
(x + y)² = 1x² + 2xy + 1y²
(x + y)³ = 1x³ + 3x²y + 3xy² +1y³
(x + y)⁴ = 1x⁴ + 4x³y + 6x²y² + 4xy³ + 1y⁴
In each expansion there is (n + 1) terms
n= 2 → (2+1) = 3 terms
n= 3 → (3+1) = 4 terms
The power of each term adds up to the power each binomial is added to (n).
For, (x + y)⁴ = 1x⁴ + 4x³y¹ + 6x²y² + 4x¹y³ + 1y⁴
Powers: (4) (4) (3+1= 4) (2+2=4) (1+3=4) (4)
where n = 4, the sum of powers are 4.
Coefficients of the expansion correspond to the Pascal's Triangle
Pascal's Triangle
*During expansion, the x and y have symmetric roles. As the powers of "x" decrease by 1, the powers of "y" increase by 1.
(x + y)⁴ = x⁴(y⁰) + 4x³y¹ + 6x²y² + 4x¹y³ + (x⁰)y⁴
To find the coefficents you can also use the formula:
nCk =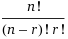
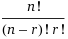
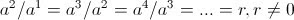
No comments:
Post a Comment