CH 9 Sequences and Series

9.1 Sequences

Infinite sequence- is a function whose domain is set of positive int

egers.

Finding the terms of a sequence

n Factorial

special case 0!=1

Factorial problems

Sigma Notation

9.2 Arithmetic Sequences and Partial Sums

A sequence is arithmetic if the differences between consecutive terms are the same.

The common difference (d) is the difference be

tween two consecutive numbers in the sequence.

Example:

4, 8, 11, 14, 17,...

d=3

Sum of a Finite Arithmetic Sequence...

9.3 Geometric Sequences and Series

A Geometric Sequence is the ratios of consecutive terms that are the same.

r is the common ratios

The sum of Geometric Sequences

if r is less that absolute value 1 then the equation is

9.5 Binomial Theorem

Binomial- a polygon that has two terms.

Expanding:

(x + y)¹ = 1x + 1y

(x + y)² = 1x² + 2xy + 1y²

(x + y)³ = 1x³ + 3x²y + 3xy² +1y³

(x + y)⁴ = 1x⁴ + 4x³y + 6x²y² + 4xy³ + 1y⁴

In each expansion there is (n + 1) terms

n= 2 → (2+1) = 3 terms

n= 3 → (3+1) = 4 terms

The power of each term adds up to the power each binomial is added to (n).

For, (x + y)⁴ = 1x⁴ + 4x³y¹ + 6x²y² + 4x¹y³ + 1y⁴

Powers: (4) (4) (3+1= 4) (2+2=4) (1+3=4) (4)

where n = 4, the sum of powers are 4.

Coefficients of the expansion correspond to the Pascal's Triangle

Pascal's Triangle

*During expansion, the x and y have symmetric roles. As the powers of "x" decrease by 1, the powers of "y" increase by 1.

(x + y)⁴ = x⁴(y⁰) + 4x³y¹ + 6x²y² + 4x¹y³ + (x⁰)y⁴

To find the coefficents you can also use the formula:

_nC_{k =}

Chapter 3 Review

Exponential Functions and Graphs:

functions:

f(x) = a^x , where a>0 and a cannot equal 0

*every exponential graph : have a horizontal asymptote @ Y=0

: has a y-intercept of 1

: no x-intercept

: domain is all read numbers (-∞, ∞)

: range of (0, ∞)

y = ab^(x-c) + d

a- causesthe graph to vertically stretch or shrink and changes y-intercept

c- causes the graph to move left or right where left moves positive and right moves more negative
d- causes the graph to move up and down

b- how fast, if less than 1 there is decay

x- a negative x causes the graph to reflect in the y-axis

Properties of Exponents:

a^x * a^y = a^(x+y)
a^x / a^y = a^(x-y)
a^-x = 1 / a^x

The Natural Base e:

f(x) = e^x
Domain: (-∞, ∞)
Range: (0, ∞)
y-intercept: (0,1)

Compound Interest:
Continuously Compounded Interest: A = Pe^rt
A = present value
P = principle value (how much invested)
r = annual rate of return (decimal form)
t = time in years

*r and t must be some time frame, the units of time must agree

Discretely Compounded Interest: A = P(1 + r/n)^nt
n = number of compounding periods per year

Logarithmic Functions

common log-

log10= log

natural log-

loge= ln

*** key to everything ***

log a x = y <--> a^y = x

log 2 16 = 4 <--> 2^4= 16

Log Graphs:

Domain: (0, ∞)

Range: (-∞, ∞)
x-intercept: (0,1)

V.A.: x=0

Transformation is log graphs:

y = alogb (x-c) + d

a= stretches graph, neg. reflects in x-axis

b= growth rate, less than 1 decrease in graph

c= moves right or left

d= moves up or down

Properties of Logs:

Summary of Exponential and Logarithmic Functions:

Chapter 5 Review

5.1 covers fundamental indentities. These are used in trigonometry to evaluate functions, simplify expressions, and solve equations. You do not need to memorize these for the final (or any other formulas from this chapter), but some examples are:

Reciprocal
csc(x)=1/sin(x)

Quotient
tan(x)=sin(x)/cos(x)

Pythagorean
sin^2(x)+cos^2(x)=1

Cofunction
sin((pi/2)-x)=cos(x)

Even/Odd
cot(-x)=-cot(x)


5.2 goes over verifying identities. Some guidelines are:

1. Work with one side of the equation at a time, preferably the more complicated side.
2. Look for opportunities to factor an expression, add fractions, square a binomial, or create a common denominator.
3. Look for opportunities to use the fundamental identities. Note which functions are in the final expression you want.
4. Try converting terms to sines and cosines.

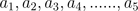
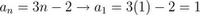
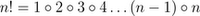
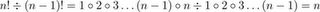
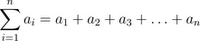
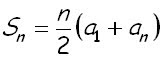
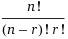
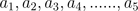
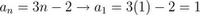
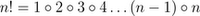
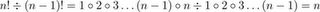
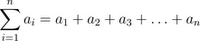
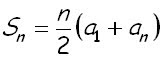
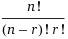
For help with sections 5.1 and 5.2: http://www.youtube.com/watch?v=pviWtesNnAY&feature=related

5.3 covers solving trigonometric equations. When solving an equation try:

1. Combining like terms
2. Taking squares and square roots
3. Factoring
4. Rewriting trigonometric functions
5. Using inverse functions

5.4 goes over the sum and difference formulas. These are used in identities and to evaluate values that aren't on the unit circle. Here are some examples:

cos(x+y)=cos(x)cos(y)-sin(x)sin(y)

sin(x+y)=sin(x)cos(y)+cos(x)sin(y)

5.5 covers multiple-angle and product-sum formulas. An example of a double-angle formula is:

• sin(2x)=2sin(x)cos(x)

An example of a power-reducing formula is:

• cos^2(x)=(1+cos(2x))/2

An example of a half-angle formula is:

• tan(x/2)=(1-cos(x))/sin(x)=sin(x)/(1+cos(x))

An example of a product-to-sum formula is:

• sin(x)cos(y)=1/2(sin(x+y)+sin(x-y))

And an example of a sum-to-product formula is:

• cos(x)+cos(y)=2cos((x+y)/2)cos((x-y)/2)

Good luck everyone!

Limits: Review

Definition of Limit:

If f(x) becomes arbitrarily close to a unique number L as x approaches c from either side, the limit of f(x) as x approaches c is L. This is written as

Lim f(x) = L
x ->c

(x approaches c, as y approaches L)

Eample:
f(x) = 2x-3
Lim f(x)
x->4

2(4) - 3
8 - 3 = 5

Lim f(x) = 5
X->4

Conditions Under Which Limits Do Not Exist:
(The limit of f(x) as x-> c does not exist if any of the following conditions is true.
1. f(x) approaches a different number from the right side of c than from the left side of c
2. f(x) increases or decreases without bound as x approaches c
3. f(x) oscillates between two fixed values as x approaches c

Properties of Limits:
(Let b and c be real numbers and let n be a positive integer)
lim b = b
x-> c

lim x = c
x->c

lim x^n = c^n
x->c



Techniques for Evaluating Limits
Evaluating Limits by Direct Substitution:
Lim (x^2 + x – 6)
x-> -1

substitute -1 in for x

(-1)^2 + (-1) – 6 = -6

Dividing out Technique:
Lim (x^2 + x – 6/x +3)

Begin by factoring the numerator and dividing out any common factors

Lim (x^2 + x – 6/x +3) = lim (x -2)(x +3)/(x + 3)
= lim (x -2)
= ((-3) – 2)
= -5
This procedure for evaluating a limit is called the dividing out technique. The validity of the procedure stems from the fact that if two functions agree at all but a single number c, they must have identical limit behavior at x = c.


Rationalizing Technique:

By direct substitution we get the indeterminate form 0/0:

In this case, we change the form of the fraction by rationalizing (eliminating the radical in) the numerator:

Therefore, by substitution, we have

Definition of Continuity
lim f(x) = lim f(x) = f(c)

x->c- x->c+

Finding a Derivative:
Find the derivative of f(x) = x^2

Definition of Limits at Infinity:
If f is a function and L1 and L2 are real numbers, the statements
Lim f(x) = L1 limit as x approaches negative infinite
X->infinite

Lim f(x) = L2 limit as x approaches infinite
x-> infinite


Limits at Infinity:

If r is a positive real integer, then
Lim 1/x^r = 0
x-> infinite

Furthermore, if x^r is defined when x<0, r =" 0"> - infinite

Comparing Limits at Infinity:
Lim -2x + 3/3x^2 = 1
x->infinite
= 0

Lim -2x^2 + 3/3x^2 = 1
x-> infinite
= -2/3

Lim -2x^3 + 3/3x^2 = 1
x-> infinite
= DNE

Evaluating Limits

There are two ways to evaulate limits.

1.) Dividing Out Technique:

Factor the numerator and denominator. Then divide out the common factors. Finally solve by direct subtitution.

Ex.

2.) Rationalizing Technique:

Multiply by the conjugate of the numerator to rationalize the limit. This allows the fraction to be written in a simpler way so that direct substitution can take place.

Ex.

How to solve limits like a pro:

http://www.youtube.com/watch?v=9GVRtS18xSk

http://www.youtube.com/watch?v=JWZwLCKyR1Q

12.1 Continued

Properties of Limits

There are 4 properties:

Lim b = b
x→ c

Lim x = c
x→ c

Lim xⁿ = cⁿ

x→ c






Ex:
(1st property)
Lim 5 = 5
x→2


(2nd property)
Lim x = 2
x→3

(3rd property)
Lim x^{2 = 9}
x→3

(4th property)

^{Lim (cubed root x) = 2}
x→8

Operations with Limits

Lim f(x) = L
x→c

and

Lim g(x) = K
x→c

Scalar Multiple:
Lim [bf(x)]= bL
x→c

Sum or difference:
Lim [f(x) ± g(x)] = L ± K

x→c

Product:
Lim [f(x)g(x0] = LK

x→c

Quotient:
Lim [f(x)/g(x)] = L/K
x→c
****with this one K can not be 0

Power:
Lim [F(x)]ⁿ = Lⁿ
x→c



Continuity

Function is continuous if:
Lim f(x) = f(a)
x→a

For extra help with continuity
http://www.youtube.com/watch?v=hlorAjS0xWE&feature=related

Introduction to Limits

Formula for limits:

f(x) becomes closer to L as x moves towards a from the left or right.

The limit of f(x) as x approaches a is L.

Example:

 

As x approaches 2, f(x) is 1. The limit is 1.  

The limit does not exist when...

1. f(x) approaches a different number from the right side of c than from the left side of c.

     - You can see below that the limit does not exist at 0 because there is a jump in the graph.

2. When the graph tends to infinity.

    - As x aproaches 3 f(x) aproaches ∞, therefore the limit does not exist.

 

3. If f(x) oscillates between two values as x aproaches c.  

Binomial Theorem

Binomial= a polygon that has two terms.

Expanding a Binomial:

(x + y)¹ = 1x + 1y

(x + y)² = 1x² + 2xy + 1y²

(x + y)³ = 1x³ + 3x²y + 3xy² +1y³

(x + y)⁴ = 1x⁴ + 4x³y + 6x²y² + 4xy³ + 1y⁴

In each expansion there is (n + 1) terms

n= 2 → (2+1) = 3 terms

n= 3 → (3+1) = 4 terms

The power of each term adds up to the power each binomial is added to (n).

For, (x + y)⁴ = 1x⁴ + 4x³y¹ + 6x²y² + 4x¹y³ + 1y⁴

Powers: (4) (4) (3+1= 4) (2+2=4) (1+3=4) (4)

where n = 4, the sum of powers are 4.

Coefficients of the expansion correspond to the Pascal's Triangle

*During expansion, the x and y have symmetric roles. As the powers of "x" decrease by 1, the powers of "y" increase by 1.

(x + y)⁴ = x⁴(y⁰) + 4x³y¹ + 6x²y² + 4x¹y³ + (x⁰)y⁴

To find the coefficents you can also use the formula:

_nC_{k =}

The 2 values next to each others' sum is equal to the number directly below the values. This is the case for all the numbers on Pascal's triangle.

Geometric Sequences and Series

A Geometric Sequence is the ratios of consecutive terms that are the same.

the number r is the common ratios of the sequence.

The difference between an Arithmaic Sequence and Geometric Sequence

Arithmatic Geometric

Geometric

The sequence whose nth term is 2^n is geometric. For this seqence, the common ratio between consecutive terms is 2.

2,4,8,16...2^n...

4/2= 2

The sum of Geometric Sequences

if r is less that absolute value 1 then the equation is s=a1/1-r

Need more help, follow the link

http://www.youtb.com/watch?v=IGFQXInm-co

soft



lv

Arithmetic Sequences and Partial Sums

Definition of an Arithmetic Sequence - a sequence whose consecutive terms have a common difference

The common difference (d) is the difference between two consecutive numbers in the sequence.

Example:

4, 8, 11, 14, 17,...

d=3

You can find the nth term of an Arithmetic Sequence by using the equation...

an = dn + c

where c = a1 -d

The equation can also be written as an = d(n-1) + a1

Example:

2, 6, 10, 14, 18

d=4

c=2

an = 4n - 2

The equation for the Sum of a Finite Arithmetic Sequence...

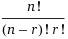
Sn = (n/2)(a1 + an)

You can use this equation to add up the numbers in a Arithmetic Sequence.

Example:

Sn = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 +.....+ 98 + 99 + 100

= (100/2)(1 + 100)
= 50(101)
=5050

You can find a Partial Sum of an Arithmetic Sequence by using the equation for the Sum of a Finite Arithmetic Sequence.

Example:

5, 16, 27, 38, 49,....
Find the 150th term

an = dn + c
a150 = 11(150) - 6
a150 = 1644

S150 = (150/2)(5 + 1644)
S150 = 75(1649)
S150 = 123,675

Sequence and Series

Definition of Sequence- An infinite sequence is a function whose domain is the set of positive integers. The funciton values

are the terms of the sequence. If the domain of the functioning consists of the first n positive integers only, the sequence is a finite sequence.


Finding the Terms of a sequence





The Fibonacci Sequence: A Recursive Sequence

Definition of Factorials- If n factorial is defined by

As a special case, zero factorial is defined as 0! = 1.

• 0!=1



• 1!=1



• 2!=1 x 2 = 2



• 3!= 1 x 2 x 3 = 6
  
  
  

Evaluating Factorial Expressions

Definition of Summation Notation- The sum of the first n terms of a sequence is represented by

Where i is called the index of summation, n is the upper limit of summation, and 1 is lower the limit of summation

Sigma Notation for Sums