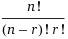Evaluating Limits

There are two ways to evaulate limits.

1.) Dividing Out Technique:

Factor the numerator and denominator. Then divide out the common factors. Finally solve by direct subtitution.

Ex.

2.) Rationalizing Technique:

Multiply by the conjugate of the numerator to rationalize the limit. This allows the fraction to be written in a simpler way so that direct substitution can take place.

Ex.

How to solve limits like a pro:

http://www.youtube.com/watch?v=9GVRtS18xSk

http://www.youtube.com/watch?v=JWZwLCKyR1Q

12.1 Continued

Properties of Limits

There are 4 properties:

Lim b = b
x→ c

Lim x = c
x→ c

Lim xⁿ = cⁿ

x→ c






Ex:
(1st property)
Lim 5 = 5
x→2


(2nd property)
Lim x = 2
x→3

(3rd property)
Lim x^{2 = 9}
x→3

(4th property)

^{Lim (cubed root x) = 2}
x→8

Operations with Limits

Lim f(x) = L
x→c

and

Lim g(x) = K
x→c

Scalar Multiple:
Lim [bf(x)]= bL
x→c

Sum or difference:
Lim [f(x) ± g(x)] = L ± K

x→c

Product:
Lim [f(x)g(x0] = LK

x→c

Quotient:
Lim [f(x)/g(x)] = L/K
x→c
****with this one K can not be 0

Power:
Lim [F(x)]ⁿ = Lⁿ
x→c



Continuity

Function is continuous if:
Lim f(x) = f(a)
x→a

For extra help with continuity
http://www.youtube.com/watch?v=hlorAjS0xWE&feature=related

Introduction to Limits

Formula for limits:

f(x) becomes closer to L as x moves towards a from the left or right.

The limit of f(x) as x approaches a is L.

Example:

 

As x approaches 2, f(x) is 1. The limit is 1.  

The limit does not exist when...

1. f(x) approaches a different number from the right side of c than from the left side of c.

     - You can see below that the limit does not exist at 0 because there is a jump in the graph.

2. When the graph tends to infinity.

    - As x aproaches 3 f(x) aproaches ∞, therefore the limit does not exist.

 

3. If f(x) oscillates between two values as x aproaches c.  

Binomial Theorem

Binomial= a polygon that has two terms.

Expanding a Binomial:

(x + y)¹ = 1x + 1y

(x + y)² = 1x² + 2xy + 1y²

(x + y)³ = 1x³ + 3x²y + 3xy² +1y³

(x + y)⁴ = 1x⁴ + 4x³y + 6x²y² + 4xy³ + 1y⁴

In each expansion there is (n + 1) terms

n= 2 → (2+1) = 3 terms

n= 3 → (3+1) = 4 terms

The power of each term adds up to the power each binomial is added to (n).

For, (x + y)⁴ = 1x⁴ + 4x³y¹ + 6x²y² + 4x¹y³ + 1y⁴

Powers: (4) (4) (3+1= 4) (2+2=4) (1+3=4) (4)

where n = 4, the sum of powers are 4.

Coefficients of the expansion correspond to the Pascal's Triangle

*During expansion, the x and y have symmetric roles. As the powers of "x" decrease by 1, the powers of "y" increase by 1.

(x + y)⁴ = x⁴(y⁰) + 4x³y¹ + 6x²y² + 4x¹y³ + (x⁰)y⁴

To find the coefficents you can also use the formula:

_nC_{k =}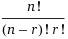

The 2 values next to each others' sum is equal to the number directly below the values. This is the case for all the numbers on Pascal's triangle.

Geometric Sequences and Series

A Geometric Sequence is the ratios of consecutive terms that are the same.

the number r is the common ratios of the sequence.

The difference between an Arithmaic Sequence and Geometric Sequence

Arithmatic Geometric

Geometric

The sequence whose nth term is 2^n is geometric. For this seqence, the common ratio between consecutive terms is 2.

2,4,8,16...2^n...

4/2= 2

The sum of Geometric Sequences

if r is less that absolute value 1 then the equation is s=a1/1-r

Need more help, follow the link

http://www.youtb.com/watch?v=IGFQXInm-co

soft



lv

Arithmetic Sequences and Partial Sums

Definition of an Arithmetic Sequence - a sequence whose consecutive terms have a common difference

The common difference (d) is the difference between two consecutive numbers in the sequence.

Example:

4, 8, 11, 14, 17,...

d=3

You can find the nth term of an Arithmetic Sequence by using the equation...

an = dn + c

where c = a1 -d

The equation can also be written as an = d(n-1) + a1

Example:

2, 6, 10, 14, 18

d=4

c=2

an = 4n - 2

The equation for the Sum of a Finite Arithmetic Sequence...

Sn = (n/2)(a1 + an)

You can use this equation to add up the numbers in a Arithmetic Sequence.

Example:

Sn = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 +.....+ 98 + 99 + 100

= (100/2)(1 + 100)
= 50(101)
=5050

You can find a Partial Sum of an Arithmetic Sequence by using the equation for the Sum of a Finite Arithmetic Sequence.

Example:

5, 16, 27, 38, 49,....
Find the 150th term

an = dn + c
a150 = 11(150) - 6
a150 = 1644

S150 = (150/2)(5 + 1644)
S150 = 75(1649)
S150 = 123,675